sandwich: Robust Covariance Matrix Estimators

Achim Zeileis, Thomas Lumley, Nathaniel Graham, Susanne Köll

Overview

The sandwich package is designed for obtaining covariance matrix estimators of parameter estimates in statistical models where certain model assumptions have been violated. More specifically, the estimators are useful in a situation where the model’s score function was correctly specified (e.g., the mean function in a linear regression model) but that the remaining likelihood was potentially misspecified (e.g., due to heteroscedasticity or a lack of independence). In this case, the usual parameter estimates are still consistent but the associated covariance matrix estimate is not, thus potentially biasing the inference such as parameter tests or confidence intervals. Luckily, there are covariance matrix estimators that are consistent under these misspecifications and that can simply be plugged in to the usual inference based on the central limit theorem. Because the covariance matrix estimators are a product of two outer “bread” matrices (based on the Hessian of the log-likelihood) and an innter “meat” matrix (based on cross-products of the corresponding score function), they are also known as “sandwich” covariances.

The sandwich package provides a wide range of such sandwich covariances in an object-oriented framework. This means that it takes the models fitted by another package without any modification or adjustment, extracts certain quantities from them, and computes the different covariance matrices based on these. For sandwich to work the model class has to provide at least an estfun() method for extracting the score matrix (containing the gradient contributions per observation) and a bread() method for extracting the inverse of some estimate of the Fisher information (that most of the “usual” covariances are based on). Some sandwich covariances also need further methods, e.g., model.matrix() or hatvalues() etc. The covariances provided are:

  • Basic sandwich() for cross-section data.
  • vcovHC() for heteroscedasticity-consistent (HC) covariances in (generalized) linear models.
  • vcovHAC() for heteroscedastiticy- and autocorrelation-consistent (HAC) covariances in time series data with convenience interfaces kernHAC() (Andrews’ kernel HAC estimator), NeweyWest(), and weave() (weighted empirical adaptive variance estimation by Lumley and Heagerty).
  • vcovCL() for clustered covariances (including multiway clustering).
  • vcovPL() and vcovPC() for panel and panel-corrected covariances.
  • vcovOPG() for outer-product-of-gradients covariances.
  • vcovBS() for bootstrap covariances (with default method and dedicated fast and more flexible methods for lm and glm objects).

These can be applied to many different model classes, including lm, glm, survreg, coxph, mlogit, polr, hurdle, zeroinfl, ivreg, betareg, and many more. (There are some exceptions, though, not all covariances are applicable to all models).

The resulting covariances can be subsequently plugged in to various functions for Wald-type inference, including coeftest(), waldtest(), and coefci() from the lmtest package or Anova(), Confint(), S(), linearHypothesis(), and deltaMethod() from car package.

Several R packages can be used to create model summary tables or visualizations based on the covariance and inference functions above. In particular broom provides a unified interface for collecting information about models, including a method for coeftest() objects. Based on broom several packages provide model summary tables with the modelsummary package being particularly versatile, including a graphical modelplot() to go along with the tabular msummary().

Installation

The stable release version of sandwich is hosted on the Comprehensive R Archive Network (CRAN) at https://CRAN.R-project.org/package=sandwich and can be installed via

install.packages("sandwich")

The development version of sandwich is hosted on R-Forge at https://R-Forge.R-project.org/projects/sandwich/ in a Subversion (SVN) repository. It can be installed via

install.packages("sandwich", repos = "https://R-Forge.R-project.org")

Publications

The package development was accompanied by three publications in the Journal of Statistical Software, describing the initial HC and HAC implementation for linear models, the corresponding object-oriented extension, and the generalization to clustered and panel covariances, respectively.

  • Zeileis A (2004). “Econometric Computing with HC and HAC Covariance Matrix Estimators.” Journal of Statistical Software, 11(10), 1-17. doi:10.18637/jss.v011.i10.
  • Zeileis A (2006). “Object-Oriented Computation of Sandwich Estimators.” Journal of Statistical Software, 16(9), 1-16. doi:10.18637/jss.v016.i09.
  • Zeileis A, Köll S, Graham N (2020). “Various Versatile Variances: An Object-Oriented Implementation of Clustered Covariances in R.” Journal of Statistical Software, 95(1), 1-36. doi:10.18637/jss.v095.i01.

Illustrations

To illustrate the functionality of the sandwich package we employ a well-known data set that was created by Petersen for benchmarking clustered standard errors. However, because the data is so simple, we will use it here to illustrate all sorts of covariances (not only clustered ones).

The data come from a simple linear regression of a response y on an explanatory variable x, but the data are clustered by firm (500 firms) and year (10 years). The data can be loaded and the model fitted by ordinary least squares (OLS):

data("PetersenCL", package = "sandwich")
m <- lm(y ~ x, data = PetersenCL)
summary(m)
## 
## Call:
## lm(formula = y ~ x, data = PetersenCL)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -6.761 -1.368 -0.017  1.339  8.678 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.0297     0.0284    1.05      0.3    
## x             1.0348     0.0286   36.20   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.01 on 4998 degrees of freedom
## Multiple R-squared:  0.208,  Adjusted R-squared:  0.208 
## F-statistic: 1.31e+03 on 1 and 4998 DF,  p-value: <2e-16

The regression summary for a linear model uses the “usual” OLS standard errors, assuming that the data are uncorrelated and homoscedastic. The summary provides partial Wald tests for the regression coefficients and also an over F test assessing all the regressors, i.e., in this case equivalent to a t test of x. To obtain the analogous tests and corresponding confidence intervals using the basic “robust” sandwich covariance for cross-section data we can combine sandwich with the lmtest package:

library("sandwich")
library("lmtest")
coeftest(m, vcov = sandwich)
## 
## t test of coefficients:
## 
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.0297     0.0284    1.05      0.3    
## x             1.0348     0.0284   36.45   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
coefci(m, vcov = sandwich)
##               2.5 % 97.5 %
## (Intercept) -0.0259 0.0853
## x            0.9792 1.0905
m0 <- lm(y ~ 1, data = PetersenCL)
waldtest(m0, m, vcov = sandwich)
## Wald test
## 
## Model 1: y ~ 1
## Model 2: y ~ x
##   Res.Df Df    F Pr(>F)    
## 1   4999                   
## 2   4998  1 1329 <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Other covariances can be plugged in analogously, potentially passing along further options for the covariance. For example, the clustered covariance vcovCL() can be used with the clustering variable firm as:

coeftest(m, vcov = vcovCL, cluster = ~ firm)
## 
## t test of coefficients:
## 
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.0297     0.0670    0.44     0.66    
## x             1.0348     0.0506   20.45   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In the same way we can compute and compare many of the other estimators in the package. A selection, mostly just with the default settings, is provided here. First, the covarainces are computed and then the corresponding standard errors extracted (square root of the diagonal):

vc <- list(
  "Standard"              = vcov(m),
  "Sandwich (basic)"      = sandwich(m),
  "Clustered"             = vcovCL(m, cluster = ~ firm),
  "Clustered (two-way)"   = vcovCL(m, cluster = ~ firm + year),
  "HC3"                   = vcovHC(m),
  "Andrews' kernel HAC"   = kernHAC(m),
  "Newey-West"            = NeweyWest(m),
  "Bootstrap"             = vcovBS(m),
  "Bootstrap (clustered)" = vcovBS(m, cluster = ~ firm)
)
t(sapply(vc, function(x) sqrt(diag(x))))
##                       (Intercept)      x
## Standard                   0.0284 0.0286
## Sandwich (basic)           0.0284 0.0284
## Clustered                  0.0670 0.0506
## Clustered (two-way)        0.0651 0.0536
## HC3                        0.0284 0.0284
## Andrews' kernel HAC        0.0437 0.0351
## Newey-West                 0.0660 0.0482
## Bootstrap                  0.0262 0.0292
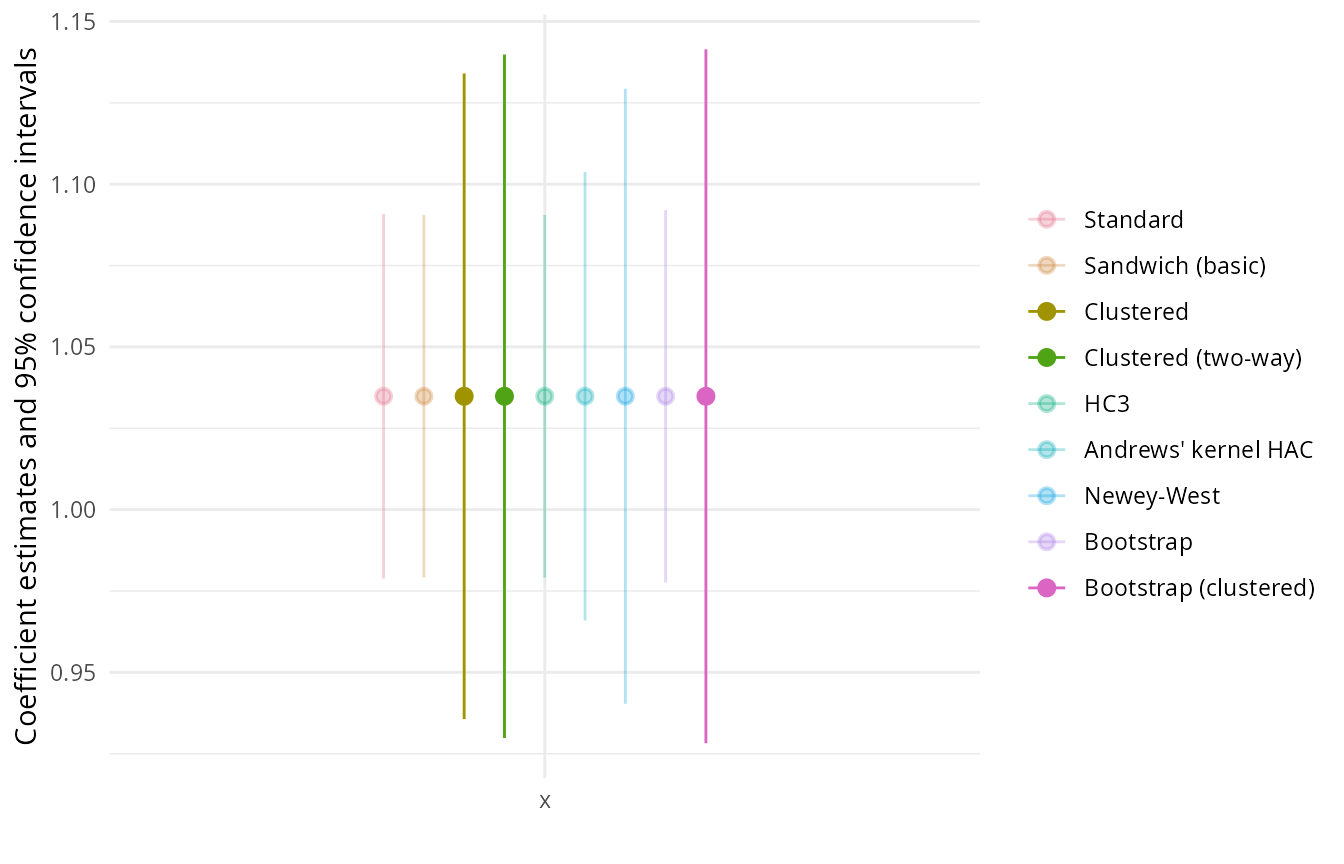
## Bootstrap (clustered)      0.0651 0.0544

This shows that due to the cluster-correlation in the data, the usual standard errors and cross-section covariances are much too small. In contrast, the different types of clustered standard errors are much larger and more appropriate here.

Tables and visualizations

For creating publication-quality tables of the model summaries using sandwich-based standard errors, we use the msummary() function from the modelsummary package. Similar to coeftest() this takes the unmodified lm() object m along with a vcov specification (starting from version 0.6.5 of the package). The latter might be specified via a covariance extractor function, certain strings (like "robust" or "HC3"), a clustering formula (like ~ firm), or simply a covariance matrix. Given that we already computed a list of covariance matrices vc above, we simply use the list element with the clustered covariance:

## `modelsummary` 2.0.0 now uses `tinytable` as its default table-drawing
##   backend. Learn more at: https://vincentarelbundock.github.io/tinytable/
## 
## Revert to `kableExtra` for one session:
## 
##   options(modelsummary_factory_default = 'kableExtra')
##   options(modelsummary_factory_latex = 'kableExtra')
##   options(modelsummary_factory_html = 'kableExtra')
## 
## Silence this message forever:
## 
##   config_modelsummary(startup_message = FALSE)
msummary(m, vcov = vc$Clustered, stars = TRUE)
tinytable_dcfxzragvabrovsmqyex
(1)
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept) 0.030
(0.067)
x 1.035***
(0.051)
Num.Obs. 5000
R2 0.208
R2 Adj. 0.208
AIC 21151.2
BIC 21170.8
Log.Lik. -10572.604
RMSE 2.00
Std.Errors Custom

The result is a nicely formatted table with content similar to the verbatim output from the corresponding coeftest() call above. (Note that in previous versions of msummary() the vcov argument was called statistic_override which is still supported for backward compatibility.)

Moreover, we can also easily produce such a model summary directly from the coeftest() output including the modified standard errors and test statistics. Even more nicely, this can also be done for a list of objects. Therefore, we use lapply() below to apply coeftest() always to the same model x = m but with the different vcov matrices from vc. The resulting list of coeftest() objects can then be displayed directly with msummary().

mlist <- lapply(vc, coeftest, x = m)
msummary(mlist)
tinytable_vet0q4shw5fgx6t72du3
Standard Sandwich (basic) Clustered Clustered (two-way) HC3 Andrews' kernel HAC Newey-West Bootstrap Bootstrap (clustered)
(Intercept) 0.030 0.030 0.030 0.030 0.030 0.030 0.030 0.030 0.030
(0.028) (0.028) (0.067) (0.065) (0.028) (0.044) (0.066) (0.026) (0.065)
x 1.035 1.035 1.035 1.035 1.035 1.035 1.035 1.035 1.035
(0.029) (0.028) (0.051) (0.054) (0.028) (0.035) (0.048) (0.029) (0.054)
Num.Obs. 5000 5000 5000 5000 5000 5000 5000 5000 5000
AIC 31141.2 31141.2 31141.2 31141.2 31141.2 31141.2 31141.2 31141.2 31141.2
BIC 63714.1 63714.1 63714.1 63714.1 63714.1 63714.1 63714.1 63714.1 63714.1

Note that this includes a reduced list of summary statistics, e.g., no R-squared. This could be changed by adding the argument save = TRUE in the lapply() call above. This would save the full model object in addition to the coeftest() output.

Finally, the different coefficients with corresponding confidence intervals can be displayed using modelplot(mlist). In the figure shown below we add some ggplot2-based customizations to the plot: omit the display for the intercepts (i.e., only show the x coefficients), flip the axes, and use a custom color palette that highlights the confidence intervals based on the disfferent clustered standard errors which are more appropriate for this data.

library("ggplot2")
pal <- hcl.colors(9, "Dark 3", alpha = c(0.3, 0.3, 1, 1, 0.3, 0.3, 0.3, 0.3, 1))
modelplot(mlist, coef_omit = "(Intercept)") + coord_flip() + scale_color_manual(values = pal)