Kernel-based HAC Covariance Matrix Estimation

A set of functions implementing a class of kernel-based heteroscedasticity and autocorrelation consistent (HAC) covariance matrix estimators as introduced by Andrews (1991).

kernHAC(x, order.by = NULL, prewhite = 1, bw = bwAndrews,
  kernel = c("Quadratic Spectral", "Truncated", "Bartlett", "Parzen", "Tukey-Hanning"),
  approx = c("AR(1)", "ARMA(1,1)"), adjust = TRUE, diagnostics = FALSE,
  sandwich = TRUE, ar.method = "ols", tol = 1e-7, data = list(), verbose = FALSE, ...)

weightsAndrews(x, order.by = NULL, bw = bwAndrews,
  kernel = c("Quadratic Spectral", "Truncated", "Bartlett", "Parzen", "Tukey-Hanning"),
  prewhite = 1, ar.method = "ols", tol = 1e-7, data = list(), verbose = FALSE, ...)

bwAndrews(x, order.by = NULL, kernel = c("Quadratic Spectral", "Truncated",
  "Bartlett", "Parzen", "Tukey-Hanning"), approx = c("AR(1)", "ARMA(1,1)"),
  weights = NULL, prewhite = 1, ar.method = "ols", data = list(), ...)

Arguments

x

a fitted model object. For bwAndrews it can also be a score matrix (as returned by estfun) directly.

order.by

Either a vector z or a formula with a single explanatory variable like ~ z. The observations in the model are ordered by the size of z. If set to NULL (the default) the observations are assumed to be ordered (e.g., a time series).

prewhite

logical or integer. Should the estimating functions be prewhitened? If TRUE or greater than 0 a VAR model of order as.integer(prewhite) is fitted via ar with method "ols" and demean = FALSE. The default is to use VAR(1) prewhitening.

bw

numeric or a function. The bandwidth of the kernel (corresponds to the truncation lag). If set to to a function (the default is bwAndrews) it is adaptively chosen.

kernel

a character specifying the kernel used. All kernels used are described in Andrews (1991).

approx

a character specifying the approximation method if the bandwidth bw has to be chosen by bwAndrews.

adjust

logical. Should a finite sample adjustment be made? This amounts to multiplication with \(n/(n-k)\) where \(n\) is the number of observations and \(k\) the number of estimated parameters.

diagnostics

logical. Should additional model diagnostics be returned? See vcovHAC for details.

sandwich

logical. Should the sandwich estimator be computed? If set to FALSE only the middle matrix is returned.

ar.method

character. The method argument passed to ar for prewhitening (only, not for bandwidth selection).

tol

numeric. Weights that exceed tol are used for computing the covariance matrix, all other weights are treated as 0.

data

an optional data frame containing the variables in the order.by model. By default the variables are taken from the environment which the function is called from.

verbose

logical. Should the bandwidth parameter used be printed?

...

further arguments passed to bwAndrews.

weights

numeric. A vector of weights used for weighting the estimated coefficients of the approximation model (as specified by approx). By default all weights are 1 except that for the intercept term (if there is more than one variable).

Details

kernHAC is a convenience interface to vcovHAC using weightsAndrews: first a weights function is defined and then vcovHAC is called.

The kernel weights underlying weightsAndrews are directly accessible via the function kweights and require the specification of the bandwidth parameter bw. If this is not specified it can be chosen adaptively by the function bwAndrews (except for the "Truncated" kernel). The automatic bandwidth selection is based on an approximation of the estimating functions by either AR(1) or ARMA(1,1) processes. To aggregate the estimated parameters from these approximations a weighted sum is used. The weights in this aggregation are by default all equal to 1 except that corresponding to the intercept term which is set to 0 (unless there is no other variable in the model) making the covariance matrix scale invariant.

Further details can be found in Andrews (1991).

The estimator of Newey & West (1987) is a special case of the class of estimators introduced by Andrews (1991). It can be obtained using the "Bartlett" kernel and setting bw to lag + 1. A convenience interface is provided in NeweyWest.

Value

kernHAC returns the same type of object as vcovHAC

which is typically just the covariance matrix.

weightsAndrews returns a vector of weights.

bwAndrews returns the selected bandwidth parameter.

References

Andrews DWK (1991). “Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation.” Econometrica, 59, 817--858.

Newey WK & West KD (1987). “A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix.” Econometrica, 55, 703--708.

Examples

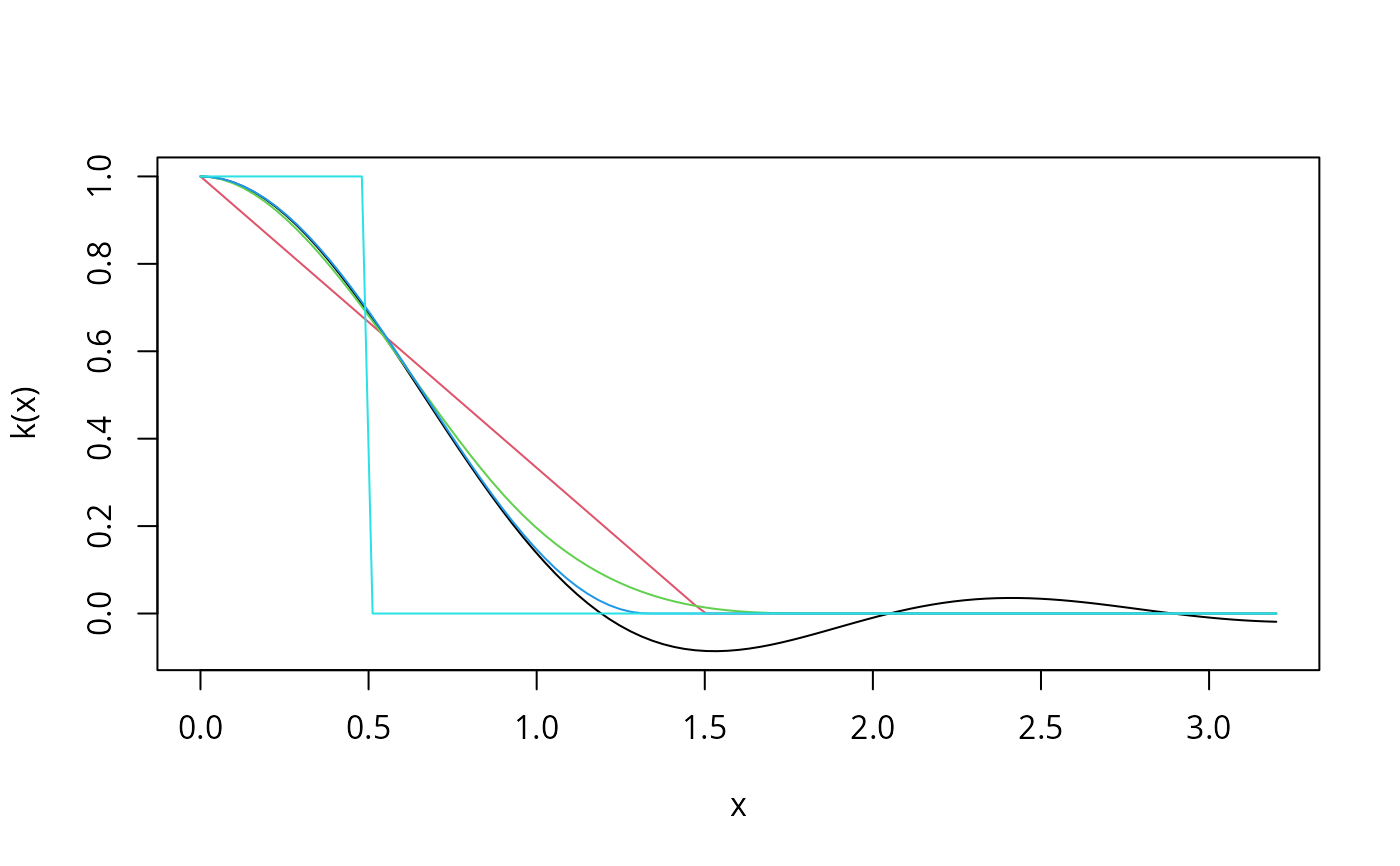
curve(kweights(x, kernel = "Quadratic", normalize = TRUE),
      from = 0, to = 3.2, xlab = "x", ylab = "k(x)")
curve(kweights(x, kernel = "Bartlett", normalize = TRUE),
      from = 0, to = 3.2, col = 2, add = TRUE)
curve(kweights(x, kernel = "Parzen", normalize = TRUE),
      from = 0, to = 3.2, col = 3, add = TRUE)
curve(kweights(x, kernel = "Tukey", normalize = TRUE),
      from = 0, to = 3.2, col = 4, add = TRUE)
curve(kweights(x, kernel = "Truncated", normalize = TRUE),
      from = 0, to = 3.2, col = 5, add = TRUE)


## fit investment equation
data(Investment)
fm <- lm(RealInv ~ RealGNP + RealInt, data = Investment)

## compute quadratic spectral kernel HAC estimator
kernHAC(fm)
#>             (Intercept)       RealGNP     RealInt
#> (Intercept) 788.6120652 -0.7502080996 49.78912814
#> RealGNP      -0.7502081  0.0007483977 -0.06641343
#> RealInt      49.7891281 -0.0664134303 17.71735491
kernHAC(fm, verbose = TRUE)
#> 
#> Bandwidth chosen: 1.744749 
#>             (Intercept)       RealGNP     RealInt
#> (Intercept) 788.6120652 -0.7502080996 49.78912814
#> RealGNP      -0.7502081  0.0007483977 -0.06641343
#> RealInt      49.7891281 -0.0664134303 17.71735491

## use Parzen kernel instead, VAR(2) prewhitening, no finite sample
## adjustment and Newey & West (1994) bandwidth selection
kernHAC(fm, kernel = "Parzen", prewhite = 2, adjust = FALSE,
  bw = bwNeweyWest, verbose = TRUE)
#> 
#> Bandwidth chosen: 2.814444 
#>             (Intercept)       RealGNP      RealInt
#> (Intercept) 608.3101258 -0.5089107386 -64.93690203
#> RealGNP      -0.5089107  0.0004340803   0.04689293
#> RealInt     -64.9369020  0.0468929322  15.58251456

## compare with estimate under assumption of spheric errors
vcov(fm)
#>             (Intercept)       RealGNP     RealInt
#> (Intercept) 620.7706170 -0.5038304429  8.47475285
#> RealGNP      -0.5038304  0.0004229789 -0.01145679
#> RealInt       8.4747529 -0.0114567949  5.61097245